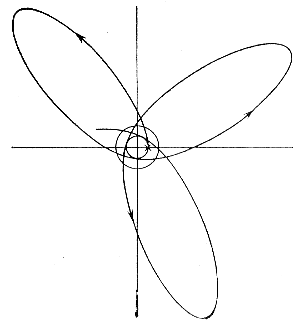
Получаемые при этом регулярные орбиты звезд имеют вид эллипсов с вращающимися линиями апсид (рис. 139). Возможны также устойчивые круговые орбиты и движения по прямым, проходящим через центр масс скопления. Плоскости орбит во всех случаях проходят через центр.
Теперь можно написать систему дифференциальных уравнений движения и проинтегрировать ее.
сила K(r), притягивающая звезду m к центру такого скопления, изменяется по закону
В таком случае M(r) легко вычисляется по формуле
Если f(r) изменяется по закону Шустера , то, принимая в нем для простоты f(0) = 1, r0 = 1, можно написать
Если f(r) - пространственная плотность звезд в скоплении на расстоянии r от его центра, то масса скопления, заключенная в сфере радиуса r,
Если пренебречь действием иррегулярных сил (влиянием близких и далеких сближений звезд с другими членами скопления), можно определить траекторию звезды, описываемую ею под действием регулярной силы, обусловленной сглаженным гравитационным полом всего скопления. Эту траекторию иногда называют регулярной орбитой. Рассмотрим регулярные орбиты звезд в сферическом скоплении, концентрирующемся к центру. Решение задачи сводится к анализу движения материальной точки с массой m вокруг точки с переменной массой M(r) (см., например, Э. Стремгрен, 1916).
Астронет > Звездные скопления
Комментариев нет:
Отправить комментарий